忍痛选修编译原理,大名鼎鼎的虎书。
Introduction
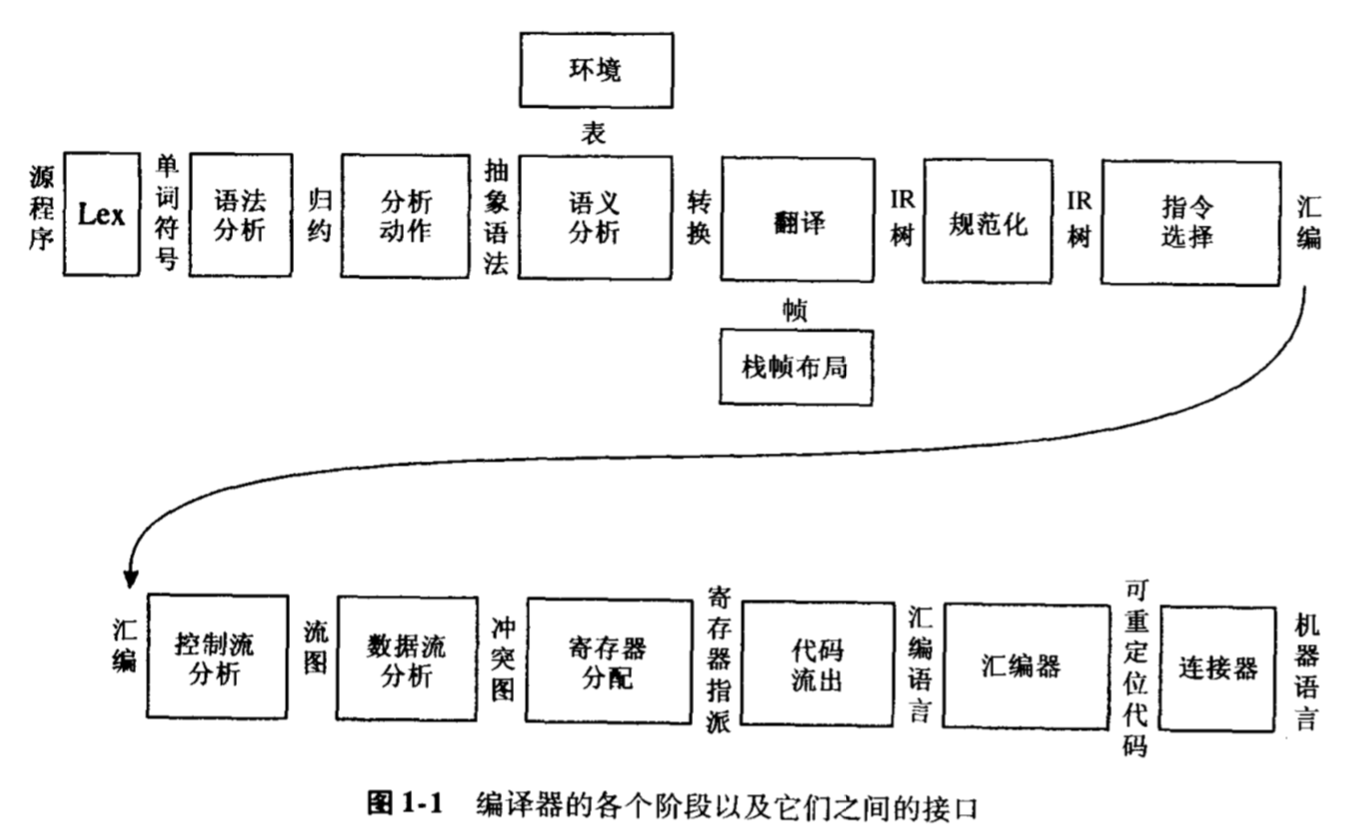
Lexical Analysis
Regular Expression
- 正则表达式可以简明扼要的描述单词(Symbol),一般而言,常用的几种语法有:+*.|[]{}。
- 在词法分析这里,正则只是用来匹配一个字符串,不强调它提取子串的功能,实际上正则引擎还支持更多的功能和操作,比如定位符,分组捕获,反向引用。
Finite Automaton
- 一个正则表达式很容易转换为非确定有限自动机(NFA)。
- 编程实现NFA不太方便,直觉上就像DFS、回溯算法等,转换成DFA会更方便程序执行。
- NFA转换DFA就是将可能走到的所有结果合并成一个状态,然后将所有可能出口作为新状态的出口。(按图来说的话,就是e线条连接的点当作一个点看待。)
Parsing
Context-Free Grammars
- 上下文无关文法,用以描述一个无限的状态。
- 这里的无限指的是递归,而且是两个表达式相互包含的递归,比如sum = expr + expr, expr = sum | digits, 这种形式的正则表达式不合法,它无法被转换为DFA。
- 上下文无关文法更强大,能够表示这种递归概念,至于如何解析并未包括。
Predicting Parsing \ LL \ LR
- 上下文无关文法所描述的状态是有二义性的,也就是满足定义的语法树不唯一,这可能会产生错误,也可能不会。
- 分析器需要选择下一步状态,预测分析就是猜测可能是什么,如果错了就回退,这个很暴力也很直接,就是速度太慢。
- LL(k)分析可以提前查看后面k个单词,再确认当前是什么状态。但对于if then else if then这种句子,k不够大的时候,LL也无法正确猜出。也就是说,LL只是多获取了固定信息,一旦预测所需信息超出这个范围,就无能为力。
- LR(k)分析会用栈存储遇到的单词,如果还不能判断状态就继续往下读取,直到可以确定。同样,在这时,对于if then,它也会有两种选择,即shift-reduce conflict。这种时候可以限定优先级或者直接指定应该采取的选择,最终达到正确需求就行。(yacc默认是shift)
Abstract Syntax
- 使用yacc生成抽象树。
- 这一章的数据结构和函数均为A开头。
Semantic Analysis
- 语义分析,实际上这一章只是检测一些语义错误,比如类型检查,recursive dec。
- 在后面会一边检查,一边将A-tree转换为IR-tree。
- 类型检查基本就是扫描树,按照语法要求就好。
Activity Record
嵌套函数(闭包)
- 书中给出三种方法:static link, display, lambda lifting。
- static link: 简单说就是做到一件事情,每次调用函数g的时候,找到g的上一级函数f(也就是函数g是在函数f内声明的),将f的frame pointer传递给g作为static link。
- 找到g的上一级,这个事情在编译时可以分析得到。知道了函数f后,通过已有的static link一定能找到f,找不到一定是定义错误。
- 有了这个static link,就可以访问外层的数据,不过一般是按顺序的,也就是会产生同名覆盖,最近优先。
Frame
- 传参限制:有一些参数总是放在寄存器里的,由于callee的使用需求,可能需要将部分参数转移到栈上。
Translation to Intermediate Code
- Translate、Frame、Temp三个主要部分。
- IR-tree中就只有三种类型,Ex,Nx,Cx。
- Ex代表“表达式”
- Nx代表“无结果语句”
- Cx代表“条件语句”
Cx
- Cx总是会有两个goto方向,有时候就会产生goto next line这种情形,有些多余。
Basic Blocks and Traces
- 现在,我们得到了IR-tree,但是它不便于分析,因为其中有ESEQ、CJUMP、CALL等语句,这会导致语句是有顺序的,不同的顺序结果不一样,从而限制了做优化的顺序。
- 我们可以通过三个步骤将IR-tree转换为等价的、无上述mismatch的形式。
- rewrite the tree into a list of canonical trees without SEQ or ESEQ nodes.
- group the list into a set of basci blocks(no jump or labels).
- order the blocks into a set of traces in which every CJUMP is immediately followed by its false label.
canon
ESEQ
简单说就是把ESEQ往上提,考虑ESEQ(s, e),移动s和e表达式的时候,只要s在e前面执行,并且最后返回值是e,ESEQ的语义就保留了。
但问题是,移动之后,s和e之间就有了其他的表达式,这些表达式的计算如果和s有关系,那么也会被s的副作用影响,而这是不对的。
我们并不总是能在编译阶段判断两个表达式之间是否有影响,这意思是说,像CONST的语句,肯定无影响,但MEM就无法判断是否是同一个数据,
所以,对于无影响的,我们就能比较简单的交换顺序,有影响的,我们可以通过多做一次MOVE来消除影响。
1
BINOP(op, e1, ESEQ(s, e2))=>ESEQ(MOVE(TEMP t, e1), ESEQ(s, BINOP(op, TEMP t, e2)));
也就是说,用中间变量保存可能受影响的变量。(我觉得这像负优化)
大致思想如上,具体算法有些复杂,不谈。
CALL
a = f1(b) + f2(c)。
像这样的式子,树结构逻辑上也没问题,但机器实现就出问题,因为函数的返回值都是用同一个寄存器(rax)来存的,连续运算两个,有一个就丢失了,然后再op就没法做。
办法和之前一样,用一个临时变量保存一下。
1
CALL(fun, args) => ESEQ(MOVE(TEMP t, CALL(fun, args)),TEMP t)
linearize
- 总之,一顿操作之后,这个seq语句就全部是顶层,不会位于其他类型节点。
- 再通过SEQ(SEQ(a,b),c) == SEQ(a,SEQ(b,c)),将seq转换为线性的一个列表。
basic block
- 入口为label,结束为jump的块。
- 从头至尾扫描语句序列,发现label就开始一个块(并结束上一个块,加上jump到这个label),发现jump就结束一个块。
trace
- 我现在才悟到,轨迹其实不是一条,它会有多条,也会有多个结果。因为很显然,有些块会有多个其他块跳过来,就像函数在不同地方被调用。(当然这里做tiger的时候,其实是面向函数体编程,也就是prog,所以这个例子不太恰当)
- 最直接的办法就是,任意选一个未被任何轨迹包括的块作为新轨迹开始,然后沿着它的跳转到下一个块,不断的做,直到形成环结束。
- 其实块变成汇编的时候,顺序是无所谓的,因为每个块都有label,重要的是,我们希望jump尽量少,同时,像循环这种,也尽量写成,预测跳转是循环体,能提高条件预测成功率。
- 对块分析trace,有助于更好的排列块和做优化。
Instruction Selection
- 每一条指令并不一定对应一个节点,它更像是对应树的一小块结构。选择指令的结果也是多样的,就像积木,不同的内部结构,搭出同样的外形。最终的结果是,指令覆盖了整个树,并且不重叠。
- 覆盖有两个概念,最优(optimum)覆盖和最佳(optimal)覆盖。
- optimal是不存在可以相邻简化的部分。
- optimum是代价之和为最小。
- optimum一定也是optimal。
Maximal Munch
- the alogrithm for optimal tiling.
- 从根节点开始,寻找合适的最大瓦片。
- 对子树进行相同算法。
- 本质上就是贪心算法,局部最优,全局不一定。
- 顺势就会想到,最优可以用动态规划,自底向上。
Abstract Assembly-Language Instructions
- 在指令选择之前,不太好决定寄存器分配,tiger在指令选择后做寄存器分配。所以我们用了一个抽象指令结构,它们不指定寄存器。
- 有AS_op,AS_move,AS_jump。
Liveness Analysis
- TODO
Register Allocate
- 寄存器分配,这一章没有太多在实现上花功夫的点,作者给出了全部伪代码。而算法本身,还是有些晦涩难懂的(主要是合并与溢出)。
图着色
- 通过将变量的冲突关系表示为图中的边,寄存器分配等价于图着色问题,这是一个np完全问题,我们采用启发式的近似算法。但是,似乎最大的把握是即使不能着色还可以将变量放到内存里(即溢出),当然这个就给优化留了不少空间。
启发式算法(K=颜色数量)
- 图中度数小于K的点,可以被去掉,并且入栈记录,不影响图可着色。
- 剩下度数大于K的点,假设它可以被去掉,也入栈记录。
- 然后栈弹出,任意分配颜色。
- 很明显,如果没有第二步,即所有点度数都小于K,那么一定能着色。
- 有了第二步,出栈时就有可能无法分配颜色,这时候就是一个溢出,需要将变量放到内存以减小它的活跃范围。
合并节点
- 合并实际上算一种优化,没有合并也能够分配成功。
- 合并的原因是两个变量有move关系,也就是在某一刻会出现a=b,并且之后b变量不再使用。那么a、b可以用同一个寄存器并省掉一次move。
- 但是很遗憾的是,不能将没有冲突(没有冲突就说明a、b不会同时活跃,第二点就成立)的move两端就全部合并,盲目合并可能使得图不可着色,我们采取保守的合并策略,简单说就是,确保这次合并不会影响图着色。
- 怎样保证呢?只要合并后的点是可被简化的,那么它肯定不影响。
- Briggs: a、b合并后的节点ab的高度数(>K)邻节点数量<=K。
- George: a的每一个邻居t,t与b已有冲突,或者t是低度数节点。
实现策略
- 合并引入了复杂度,有这样一个问题,先合并还是先简化?
- 先简化,那么显然,不要直接将move相关的点给简化掉了,那样就少了一次合并机会。
- 先合并,很显然,合并失败的可能性会很大,在极端情况下甚至等同于先简化后合并。
- 书上采用了先简化的策略,并且规定不能简化传送相关的点,但是有些传送相关的点也不能被合并,所以引入了冻结(freeze),就是将一个点变为传送无关(放弃尝试合并,变为可简化的)。
- 当简化、合并、冻结都无法进行,那么图中就全是传送无关的高度数节点,此时采用溢出,假设它可以着色,强行入栈。
- 最后出栈分配颜色,如果遇到无法分配的,先记录下来,继续分配,最后重写程序,从活跃分析开始重来一次。
预着色节点
- 图中会有一些节点,代表的就是真实寄存器,比如rax,六个参数寄存器,callee-save寄存器等,这些在codegen时会被显式使用到,所以不可避免地会出现在图中。
- 它们不应该被合并,也不能被简化,它们具有特定颜色。
- 它们的活跃范围必须很小,要是真实寄存器的活跃范围都很大,那么还怎么分配寄存器给临时变量呢,它们一定会有很多冲突。
- 活跃范围主要靠move给一个新的临时变量,过程结束再move回来,这样它在这个过程中就是不活跃的。
- 实际上,临时变量和真实寄存器一定会被合并,随后的溢出是源于局部变量的分配,当出现call指令,会再用到真实寄存器,call节点上所有量都是活跃的,这时候局部变量和真实寄存器就会冲突,局部变量还会和临时变量冲突,导致必然出现溢出。由于临时变量度数大,所以会先入栈,反而会得不到颜色,导致真实溢出,最后被替换掉。
- 非callee-save的寄存器活跃范围,需要在call指令的时候,将它们放到call的dst,表示不是跨过程活跃。这样会使得它们与跨过程活跃临时变量冲突,临时变量就会被迫先分配callee-save,如果都不够用,就会溢出。
x86-64的特点思考
一个非常trick的点,如果一个函数内,既有局部变量,又有call指令,那么它一定会产生溢出。
- 如果局部变量放到非callee-save,那么call的时候会冲突。
- 如果放到callee-save,放之前callee-save会冲突(也就是必须为自己的caller保存这些寄存器)。
很令人感到困惑,十六个寄存器竟然还这么多溢出,但是仔细想想确实是这样。